⚙️ Procedural Animation: Locomotion (Part 2)
In Part 1 we took care of the preliminaries, setting up our assets, and getting a base layer root and hip motion going on which to start grooving. In this part we’ll take the next step and start stepping.

One of the famous Eadweard Muybridge photos.
First things first, to simplify things, let’s refactor our code for the legs into helper structs so that we don’t have to copy-paste each line for both the left and right legs.
struct FootController
{
FVector RestPos;
bool IsLeft( const ALocoPawn& Pawn ) const { return this == &Pawn.FootL; }
FVector& RefPos( ALocoPawn& Pawn ) const { return IsLeft( Pawn ) ? Pawn.FootPosL : Pawn.FootPosR; }
void Init( ALocoPawn& Pawn );
void Update( ALocoPawn& Pawn, float DeltaTime );
};
FootController FootL;
FootController FootR;
// LocoPawn.cpp
void ALocoPawn::FootController::Init( ALocoPawn& Pawn )
{
RestPos = RefPos( Pawn );
}
void ALocoPawn::FootController::Update( ALocoPawn& Pawn, float DeltaTime )
{
const FTransform& ToWorld = Pawn.GetActorTransform();
FVector& Pos = RefPos( Pawn );
Pos = ToWorld.TransformPosition( RestPos );
Pos.Z = 0.0f;
Pos = ToWorld.InverseTransformPosition( Pos );
}
Rather than trying to fully puzzle-out stepping all at once, I thought I’d start with the simplest idea: we already implemented hip-swaying last week. What if we just pick up our feet in sync with the sway?
UPROPERTY( EditDefaultsOnly, BlueprintReadWrite )
float StepHeight = 75.0f;
// LocoPawn.cpp
void ALocoPawn::FootController::Update( ALocoPawn& Pawn, float DeltaTime )
{
const FTransform& ToWorld = Pawn.GetActorTransform();
FVector& Pos = RefPos( Pawn );
float RadiansOffset = IsLeft( Pawn ) ? 0.0f : PI;
float Radians = FMath::Fmod( 0.5f * Pawn.HipPhase * 2.0f * PI + RadiansOffset, 2.0f * PI );
float Arc = FMath::Max( 0.0f, Pawn.HipMulti * FMath::Sin( Radians ) );
Pos = ToWorld.TransformPosition( RestPos );
Pos.Z = Pawn.StepHeight * Arc;
Pos = ToWorld.InverseTransformPosition( Pos );
}
- We take the
Maxof the of the sway oscillation and 0 to ensure that the foot is flat at Z=0 during the off-cycle. - We stagger the right foot by adding
PI(180 degrees) to its phase.

To be honest, my expectations were low, but this doesn’t look too bad. ⛸️
There’s an obvious flaw with this version: the feet are sliding on the ground like ice-skates. But there’s also a subtle flaw: the feet are making contact directly-below the body, as opposed to out in front. So we need to make two changes:
- Pin the foot to world-space when in contact with the ground.
- Extrapolate the target step position ahead of the body.
UPROPERTY( EditDefaultsOnly, BlueprintReadWrite )
float StepExtrap = 0.15;
struct FootController
{
...
FVector PinnedPos;
bool bPinned;
};
// LocoPawn.cpp
void ALocoPawn::FootController::Init( ALocoPawn& Pawn )
{
...
PinnedPos = ToWorld.TransformPosition( RestPos );
bPinned = true;
}
void ALocoPawn::FootController::Update( ALocoPawn& Pawn, float DeltaTime )
{
...
Pos = ToWorld.TransformPosition( RestPos );
Pos += Pawn.StepExtrap * Pawn.Velocity; // offset step-target out-front
Pos.Z = 0.0f;
// pin status changed?
bool bWantPin = Radians >= PI;
if( bPinned != bWantPin )
{
if( bWantPin )
PinnedPos = Pos;
else
PinnedPos = ToWorld.InverseTransformPosition( PinnedPos );
bPinned = bWantPin;
}
// apply current status
if( bPinned )
{
Pos = ToWorld.InverseTransformPosition( PinnedPos );
}
else
{
float X = 0.5f - 0.5f * FMath::Cos( Radians );
Pos.Z += Pawn.StepHeight * Arc;
Pos = FMath::Lerp( PinnedPos, ToWorld.InverseTransformPosition( Pos ), X );
}
}
I chose Cos(Radians) for the horizontal stepping interpolation, because the height is Sin(Radians), so that would produce a circular arc, which I thought might look good?
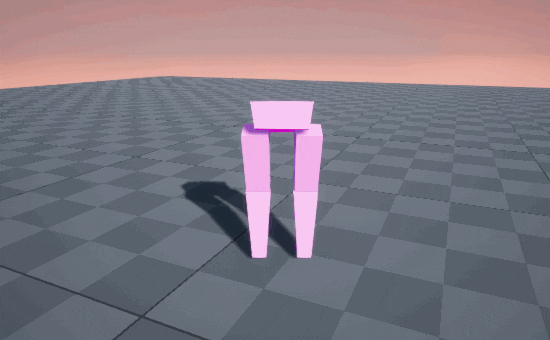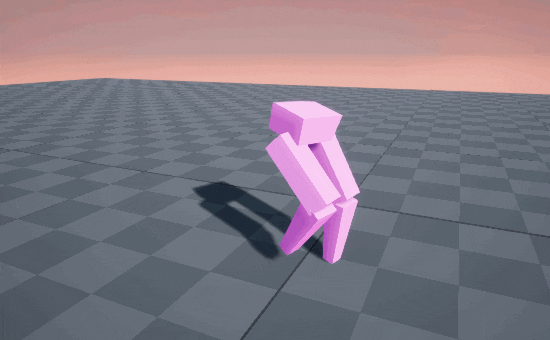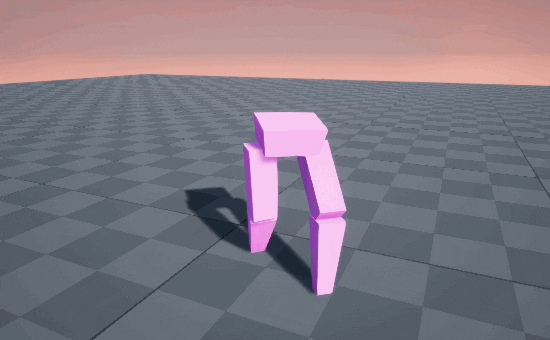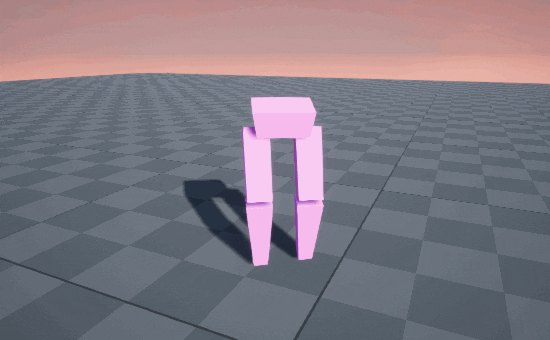
STOMP! STOMP! STOMP! 🥾
So circular arcs produce a stomping gait, because the end of the motion is straight-down into the ground. But when we’re walking normally, we’re usually straighening out our knee on the descent, causing our feet to glide into contact with the ground, like an airplane landing.

To translate this to code, I noodled around with the Desmos Graphing Calculator until I found a StepArc graph which matches our animation onion-skin, on the normalized [0-1] range.

I can’t quite explain the art of designing graphs; I’ve just been praticing since I first played Green Globs in middle school. In this case I was combining an up-down arc with an ease-out curve.
float StepArc( float X )
{
// simplified version of the graph we designed
float _X = ( 1.0f - X );
return 9.481481481f * _X * _X * _X * X;
}
void ALocoPawn::FootController::Update( ALocoPawn& Pawn, float DeltaTime )
{
...
{
float X = FMath::Min( 1.0f, Radians / PI );
Pos.Z += Pawn.StepHeight * Pawn.HipMulti * StepArc( X );
Pos = FMath::Lerp( PinnedPos, ToWorld.InverseTransformPosition( Pos ), X );
}
}
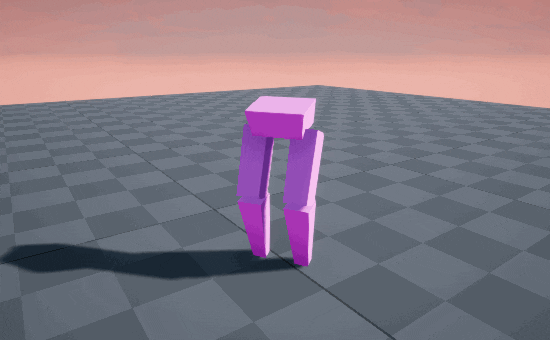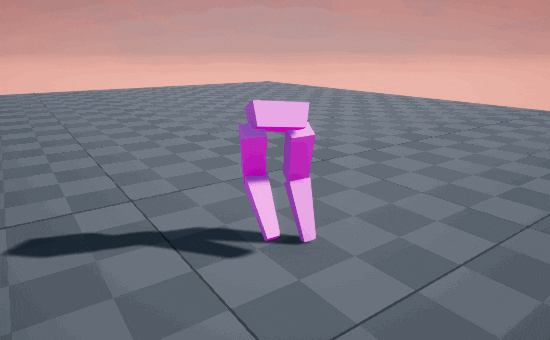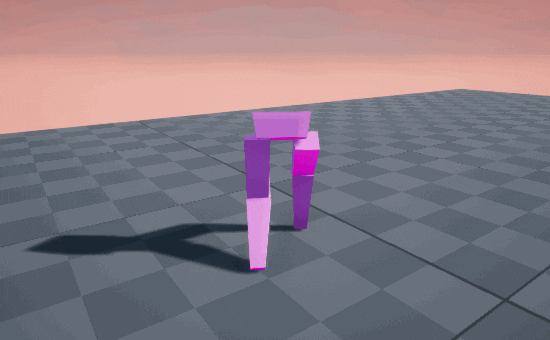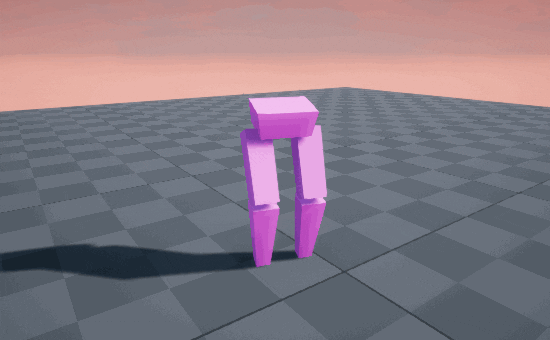
Smooth as silk! 🦵
We could of course interpolate the two step arcs with a control parameter called stompiness if our game design calls for it.
This looks great, so that’s a good place to leave it for now, but one last piece of foreshadowing: to get results looking this nice, I did have to dial-down the movement speed by more than half. The root position was cruising at sprinting speeds before, and the step-frequency required to keep up resembled a Benny Hill sketch.

The reason is because our whole mental model up until this point has describe how people walk, but not how they run. In Part 3 we’ll revise our mental model and introduce changes at each layer to enable sprinting. Thank you for reading! 💖
Full Sample Code for Part 2 here.