⚙️ Procedural Animation: Inverse Kinematics

Procedural animation is a priority on Tiny Starpilot. As a designer, I like how it it improves the responsiveness and “juiceness” of interactive characters. As a programmer, it’s my area of professional expertise. Finally, as a solo dev, it lets me create more “modular” assets which can be shared between characters with different skeletons.

The biggest tool in the procedural-animation toolkit is called Inverse Kinematics. With these algorithms, designers can specify “targets” (often called effectors) for the animation system, and joints are internally rotated to satisfy those goals.

Footage of Modular Animations

An example of my modular-design: anim nodes automatically discover and coordinate with very little explicit setup.

Unreal has built-in IK, Control Rig, but I’ve chosen to write my own solvers both so that I can produce tighter results than their generic FABRIK solver, and to reduce the amount of boilerplate blueprint noodling.

A full study of IK would fill a college degree, so just to give a taste let’s break-down the simplest but most-common type of IK: two-bone solving. I use these to pose legs when generating locomotion, and to pose arms when aiming or grasping.

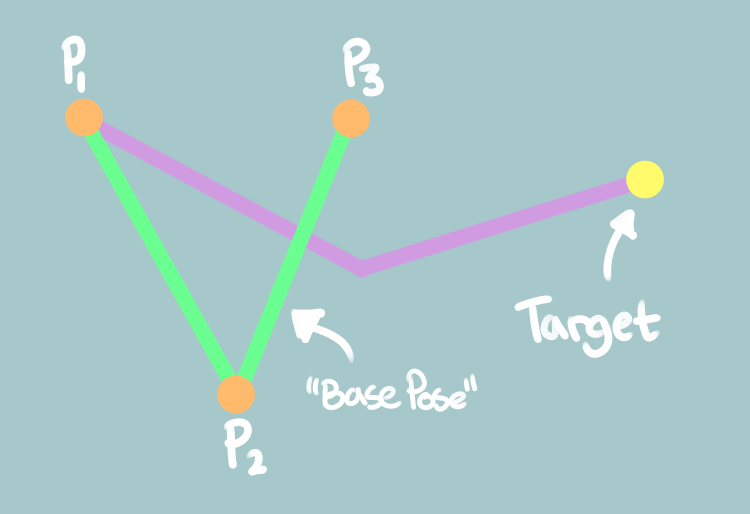
Given a “Base Pose” for a limb, compute the smallest shoulder/elbow rotation which places the point P3 onto the Target Effector.

What makes this case simple is that, unlike many other problems in kinematics, there is an analytical solution! It’s based on the Law of Cosines!

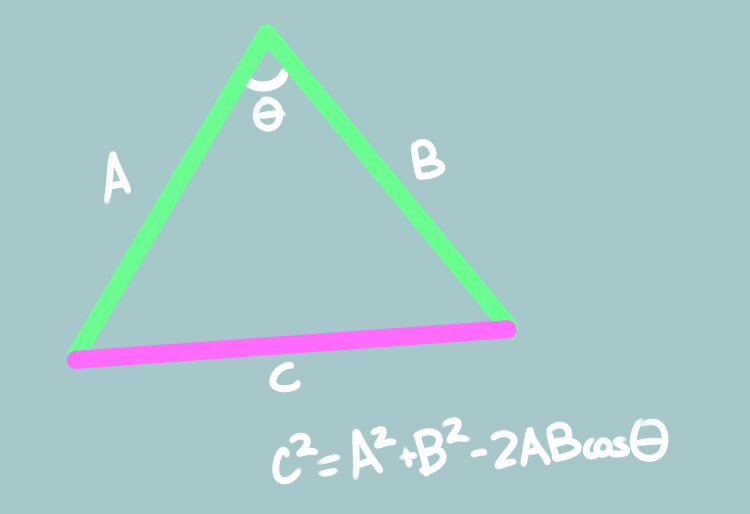
Given the length of your arm bones (A & B), and the offset from your shoulder to your hand (C), we can compute the angle you elbow makes (θ).

Applying this in code introduces two wrinkles:

How do we translate from the flat plane to 3D spatial coordinates?
How do we convert the angles into 3D orientations?

Let’s start writing code and I’ll give you those answers in context. Let’s start by declaring a helper-struct with all our inputs:

struct FTwoBoneSolver
{
	FTransform Root; // shoulder
	FTransform Mid;  // elbow
	FTransform End;  // hand

	void Solve( const FVector& Target ); // updates transforms in-place
};

FTransform is Unreal’s Position/Rotation/Scale structure.

A quick note at this point – all the joint transforms are in the same-coordinate space (in Animation Blueprints I use Component Space for everything). If you have relative transforms you’ll need to compose them, like so:

FTwoBoneSolver Solver;
// convert relative transforms to same coordinate space
Solver.Root = LocalShoulder;
Solver.Mid = LocalElbow * Solver.Root;
Solver.End = LocalHand * Solver.Mid;

...

// restore transform to relative local space
ShoulderTransform = Solver.Root;
ElbowTransform = Solver.Mid.GetRelativeTransform( Solver.Root );
HandTransform = Solver.End.GetRelativeTransform( Solver.Mid );

Note that Unreal FTransforms use transposed ( Child * Parent ) multiplication order (ugh)!

Now for the actual implementation, we start by saving the intial positions of the joints, and computing the bone lengths:

void FTwoBoneSolver::Solve( const FVector& Target )
{
	// input pose
	FVector InEndLoc = End->GetLocation();
	FVector InMidLoc = Mid->GetLocation();
	FVector InRootLoc = Root->GetLocation();
	float UpperLen = FVector::Dist( InRootLoc, InMidLoc );
	float LowerLen = FVector::Dist( InMidLoc, InEndLoc );
	float MaxLength = UpperLen + LowerLen - 1.0f;

Max Length is the maximum offset we can take the hand from the shoulder. This can’t be longer than the arm itself (unless you allow stretching), and I actually clamp it 1cm shorter to avoid some edge-cases which creep in when all three joints snap into a straight line, and you can’t determine their plane.

The next step is to recognize that the three points lie on a flat plane, and can be decomposed into two orthogonal “basis vectors” (ToEnd and the Pole Vector).

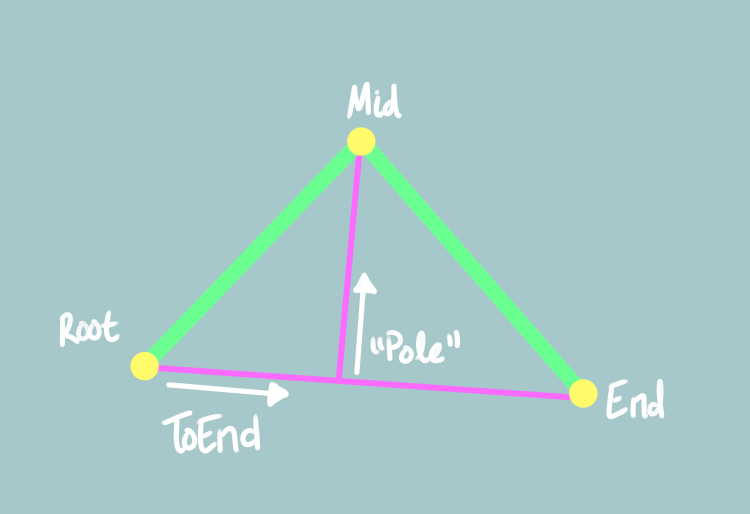
All our 2D geometry will be multiplied by vectors to become 3D coordinates.

	FVector ToEnd = ( InEndLoc - InRootLoc ).GetSafeNormal();
	FVector InPoleVec = FVector::VectorPlaneProject( InMidLoc - InRootLoc, ToEnd );
	InPoleVec.Normalize();

Next we compute the Swing rotation from ToEnd to ToTarget. This rotation is a Quaternion, which is just a technical way of encoding an Angle-Axis Rotation. Internally FindBetween() is using the cross-product to compute the axis of rotation and the dot-product to compute the angle.

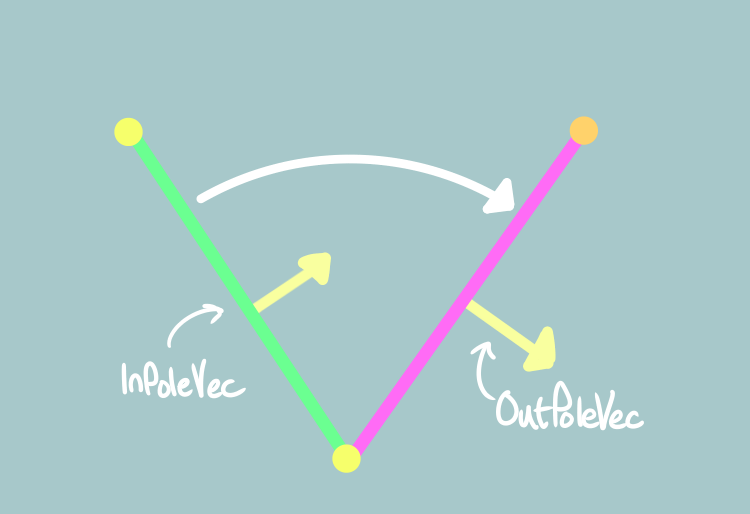
	FVector TargetOffset = ( Target - InRootLoc ).GetClampedToMaxSize( MaxLength );
	float TargetDist = TargetOffset.Size(); // we'll want this later
	FVector ToTarget = TargetOffset / TargetDist;
	FQuat ToTargetSwing = FQuat::FindBetweenNormals( ToEnd, ToTarget );
	FVector OutPoleVec = ToTargetSwing * InPoleVec;

Note that ( Quaternion * X ) is a shorthand for Quaternion.RotateVector( X ).

Now we have all the inputs to the Law of Cosines, as well as the vectors to convert them from 2D to 3D.

A = TargetDist
B = UpperLen
C = LowerLen

Rearrange the terms to solve for θ, the angle the Upper Arm bone will make with the ToTarget direction:

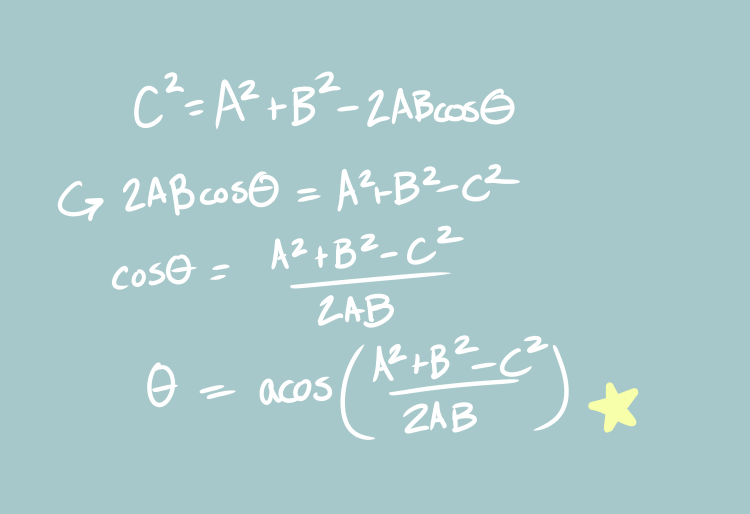
When we plug this in we calculate the denominator first, so we can check for a divide-by-zero edge case:

	float Denom = 2.0f * UpperLen * TargetDist;
	float CosAngle = 0.0f;
	if( Denom > KINDA_SMALL_NUMBER )
		CosAngle = ( TargetDist*TargetDist + UpperLen*UpperLen - LowerLen*LowerLen ) / Denom;
	float Angle = FMath::Acos( CosAngle );

From here it’s just some trigonometry to determine the offsets along the ToTargetDir and OutPoleVec basis directions (recall that cosθ and sinθ are the horizontal and vertical components of a 2D unit direction vector):

	float PoleDist = UpperLen * FMath::Sin( Angle );
	float TargetDist = UpperLen * CosAngle;
	FVector OutEndLoc = InRootLoc + TargetOff;
	FVector OutMidLoc = InRootLoc + TargetDist * ToTargetDir + PoleDist * OutPoleVec;

So now we have the new end and mid positions (the shoulder doesn’t move). To convert these to rotations we use the same FindBetween() functions, comparing the old and new directions. Do note that the MidSwing is downstream from the RootSwing, and therefore needs to combine both rotations.

	FVector ToMidIn = InMidLoc - InRootLoc;
	FVector ToMidOut = OutMidLoc - InRootLoc;
	FQuat RootSwing = FQuat::FindBetween( ToMidIn, ToMidOut );
	FVector InEndLoc_WithRootSwing = InRootLoc + RootSwing * ( InEndLoc - InRootLoc );
	FVector ToEndIn = InEndLoc_WithRootSwing - OutMidLoc;
	FVector ToEndOut = OutEndLoc - OutMidLoc;
	FQuat MidSwing = FQuat::FindBetween( ToEndIn, ToEndOut ) * RootSwing;

Unlike FTransforms, FQuats use the textbook ( Parent * Child ) multiplication order (YOLO)

And the last thing we do is write the results:

	Root->SetRotation( RootSwing * Root->GetRotation() );
	Mid->SetLocation( OutMidLoc );
	Mid->SetRotation( MidSwing * Mid->GetRotation() );
	End->SetLocation( OutEndLoc );
	End->SetRotation( MidSwing * End->GetRotation() );
}

Before we wrap, I’ll show you a snippet of this code in use to clarify what I meant up top by writing custom code to get “tighter results” with less “boilerplate.” Here’s the actual Animation Evaluation code for the arm-aiming modifier. The solver gets the arm in basically the right pose, and then we apply a small FindBetween() fixup rotation to swing the whole arm so the forearm direction matches your shooting direction.

Footage of the Ace Fighter Strafing and Shooting

Pew, pew, pew!

void FAnimNode_ArmAim::EvaluateSkeletalControl_AnyThread( FComponentSpacePoseContext& Output, TArray<FBoneTransform>&  OutBoneTransforms )
{
	// initialize with the base pose from the previous anim node
	FTwoBoneSolver Solver;
	Solver.Root = Output.Pose.GetComponentSpaceTransform( ShoulderIdx );
	Solver.Mid = Output.Pose.GetComponentSpaceTransform( ElbowIdx );
	Solver.End = Output.Pose.GetComponentSpaceTransform( WristIdx );

	// extent arm almost-full (99%) towards the target
	float Length = 0.99f * (
		FVector::Dist( Solver.Root.GetLocation(), Solver.Mid.GetLocation() ) +
		FVector::Dist( Solver.Mid.GetLocation(), Solver.End.GetLocation() )
	);
	Solver.Solve( Solver.Root.GetLocation() + AimingDir * Length );
	
	// align the elbow->hand direction to the aiming direction
	FVector ForearmDir = Solver.End.GetLocation() - Solver.Mid.GetLocation();
	FQuat Fixup = FQuat::FindBetween( ForearmDir, AimingDir );
	Solver.Mid.SetLocation( Solver.Root.GetLocation() + Fixup * ( Solver.Mid.GetLocation() - Solver.Root.GetLocation() ) );
	Solver.End.SetLocation( Solver.Root.GetLocation() + Fixup * ( Solver.End.GetLocation() - Solver.Root.GetLocation() ) );
	Solver.Root.SetRotation( Fixup * Solver.Root.GetRotation() );
	Solver.Mid.SetRotation( Fixup * Solver.Mid.GetRotation() );
	Solver.End.SetRotation( Fixup * Solver.End.GetRotation() );

	OutBoneTransforms.SetNumUninitialized(3);
	OutBoneTransforms[0] = FBoneTransform( ShoulderIdx, Solver.Root );
	OutBoneTransforms[1] = FBoneTransform( ElbowIdx, Solver.Mid );
	OutBoneTransforms[2] = FBoneTransform( WristIdx, Solver.End );
}

Fun fact: Unreal can evaluate FAnimNodes on background threads in parallel, so we can actually go a bit hog-wild with the math.

UPDATE: Here’s a complete listing of the same code for the Unity Game Engine in C#:

using UnityEngine;

public struct JointPose {
	public Vector3 position;
	public Quaternion rotation;
}

public struct TwoBoneIK {
	public JointPose root;
	public JointPose mid;
	public JointPose end;

	public void Solve( Vector3 InTargetPos ) {
		var InEndLoc = end.position;
		var InMidLoc = mid.position;
		var InRootLoc = root.position;
		var UpperLen = Vector3.Distance( InRootLoc, InMidLoc );
		var LowerLen = Vector3.Distance( InMidLoc, InEndLoc );
		var MaxLength = UpperLen + LowerLen - 0.01f;

		var ToEnd = ( InEndLoc - InRootLoc ).normalized;
		var InPoleVec = Vector3.ProjectOnPlane( InMidLoc - InRootLoc, ToEnd ).normalized;

		var ToTargetOffset = ( InTargetPos - InRootLoc );
		if( ToTargetOffset.sqrMagnitude > MaxLength * MaxLength )
			ToTargetOffset = ToTargetOffset.normalized * MaxLength;
		var ToTargetDist = ToTargetOffset.magnitude;
		var ToTarget = ToTargetOffset / ToTargetDist;
		
		var ToTargetSwing = Quaternion.FromToRotation( ToEnd, ToTarget );
		var OutPoleVec = ToTargetSwing * InPoleVec;

		var Denom = 2.0f * UpperLen * ToTargetDist;
		var CosAngle = 0.0f;
		if( Denom > Mathf.Epsilon )
			CosAngle = ( ToTargetDist*ToTargetDist + UpperLen*UpperLen - LowerLen*LowerLen ) / Denom;

		var Angle = Mathf.Acos( CosAngle );
		var PoleDist = UpperLen * Mathf.Sin( Angle );
		var EffDist = UpperLen * CosAngle;

		var OutEndLoc = InRootLoc + ToTargetOffset;
		var OutMidLoc = InRootLoc + EffDist * ToTarget + PoleDist * OutPoleVec;

		var InToMid = InMidLoc - InRootLoc;
		var OutToMid = OutMidLoc - InRootLoc;
		var RootSwing = Quaternion.FromToRotation( InToMid, OutToMid );
		var InEndLoc_WithRootSwing = InRootLoc + RootSwing * ( InEndLoc - InRootLoc );
		var ToInEnd = InEndLoc_WithRootSwing - OutMidLoc;
		var ToOutEnd = OutEndLoc - OutMidLoc;
		var MidSwing = Quaternion.FromToRotation( ToInEnd, ToOutEnd ) * RootSwing;

		root.rotation = RootSwing * root.rotation;
		mid.position = OutMidLoc;
		mid.rotation = MidSwing * mid.rotation;
		end.position = OutEndLoc;
		end.rotation = MidSwing * end.rotation;
	}
}

Thanks for reading! ❤️

2023-02-26

https://blog.littlepolygon.com/posts/twobone/ Max Kaufmann

#tech